Posts by Collection

Classical Limit for the Varying-Mass Schrödinger Equation with Random Inhomogeneities

Published in Journal of Computational Physics, August 2021

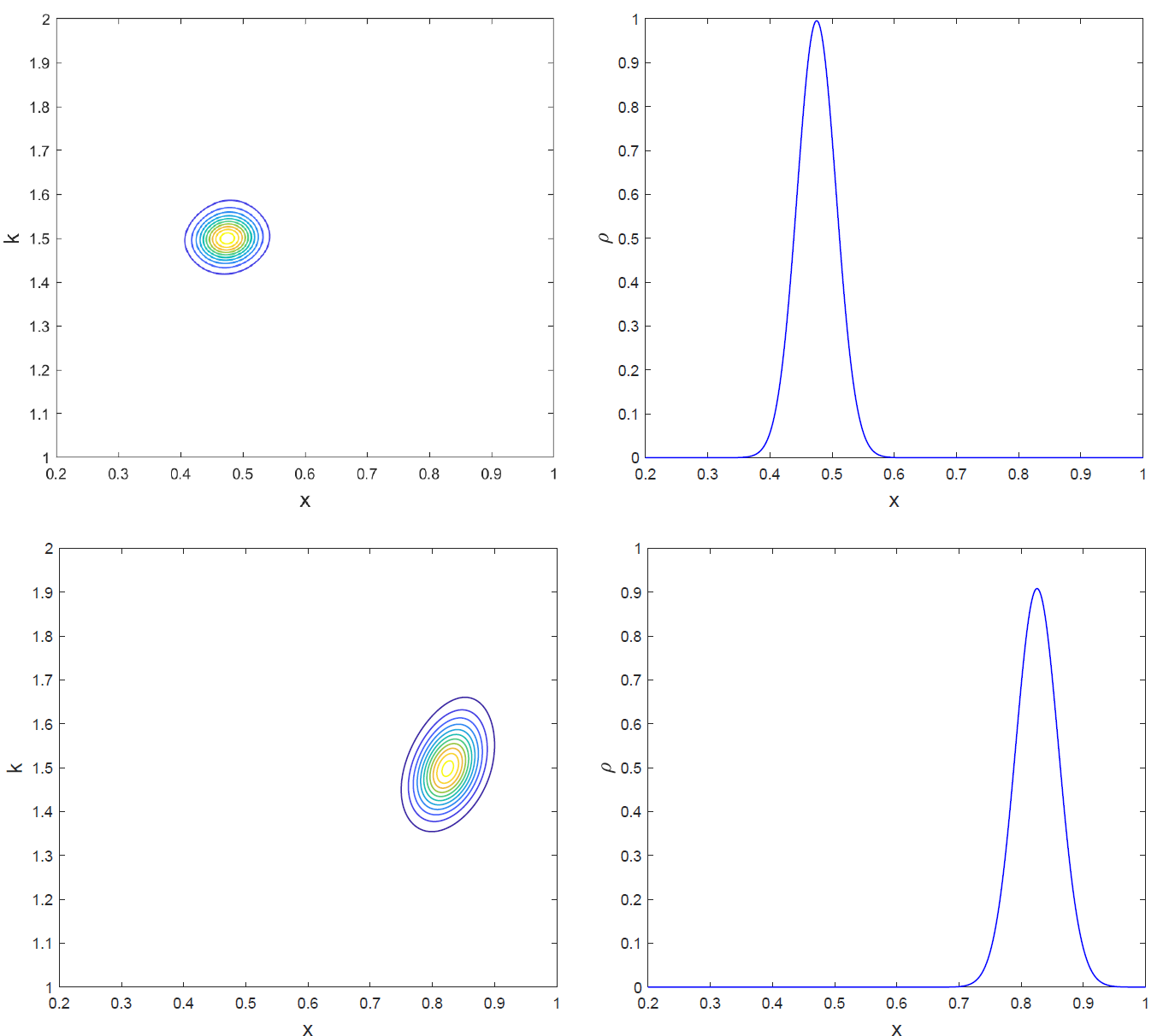
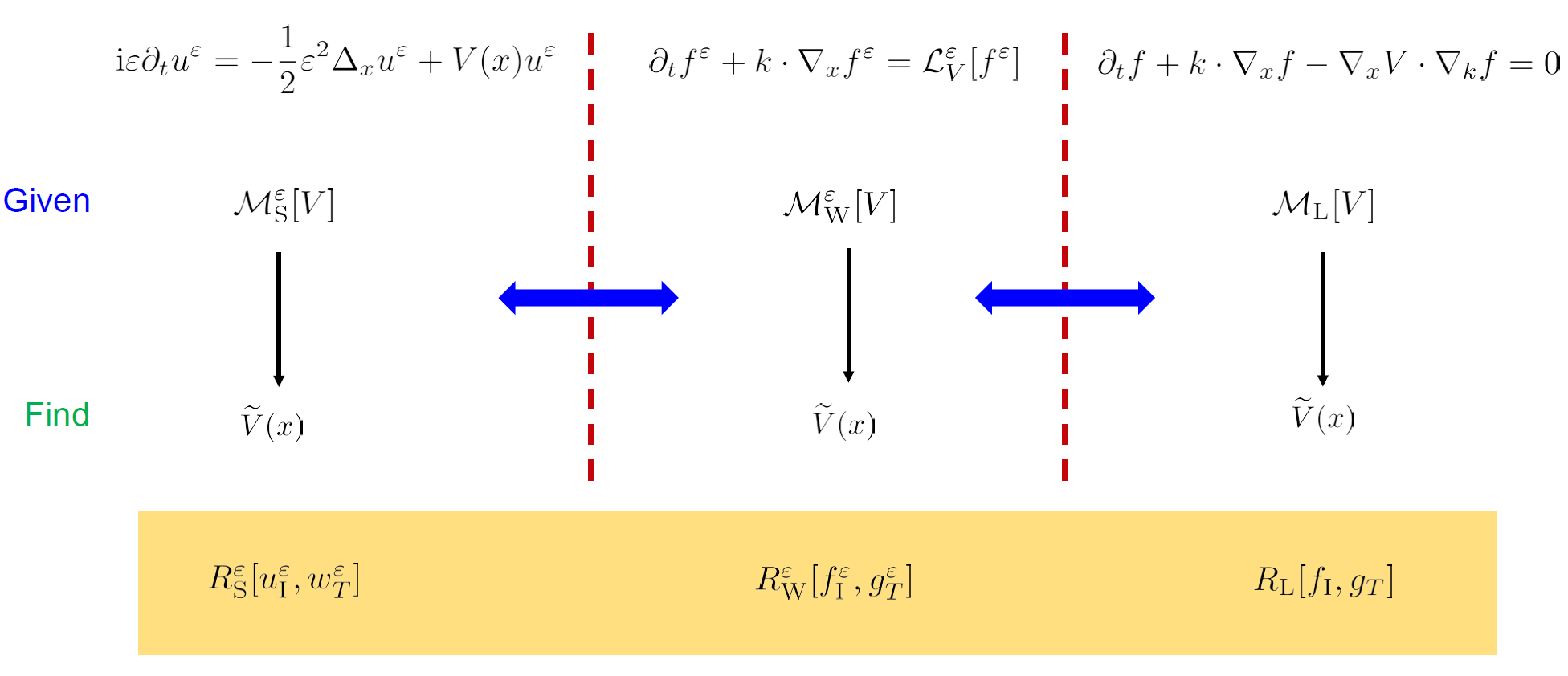
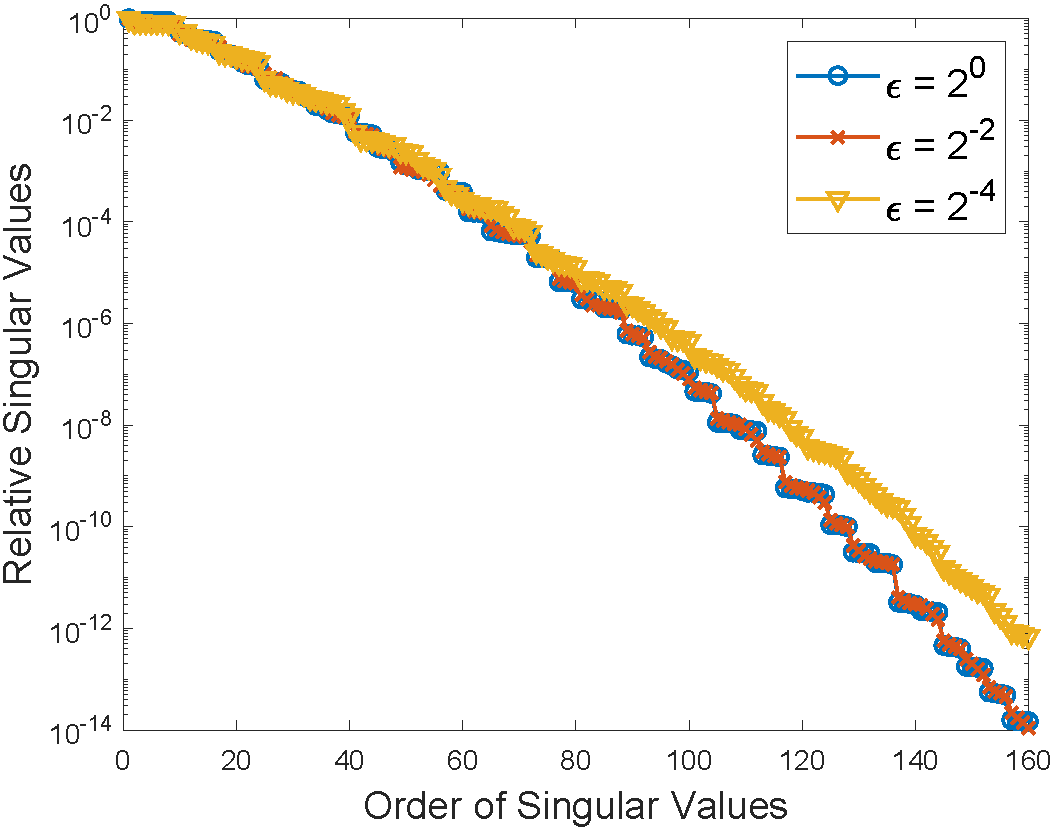
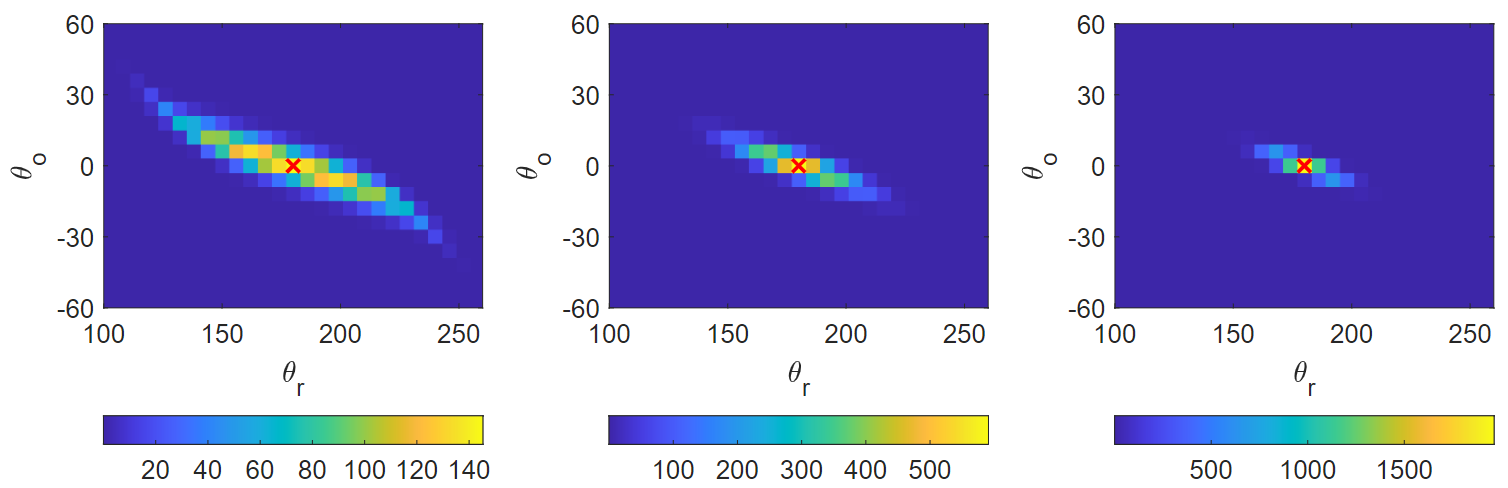
The varying-mass Schrödinger equation (VMSE) has been successfully applied to model electronic properties of semiconductor hetero-structures, for example, quantum dots and quantum wells. In this paper, we consider VMSE with small random heterogeneities, and derive a radiative transfer equation as its asymptotic limit. The main tool is to systematically apply the Wigner transform in the classical regime when the rescaled Planck constant , and expand the Wigner equation to proper orders of $\varepsilon\ll 1$. As a proof of concept, we numerically compute both VMSE and its limiting radiative transfer equation, and show that their solutions agree well in the classical regime.

Joint work with Qin Li and Xu Yang.

State-Specific Projection of COVID-19 Infection in the United States and Evaluation of Three Major Control Measures

Published in Scientific Reports, December 2020

Most models of the COVID-19 pandemic in the United States do not consider geographic variation and spatial interaction. In this research, we developed a travel-network-based susceptible-exposed-infectious-removed (SEIR) mathematical compartmental model system that characterizes infections by state and incorporates inflows and outflows of interstate travelers. Modeling reveals that curbing interstate travel when the disease is already widespread will make little difference. Meanwhile, increased testing capacity (facilitating early identification of infected people and quick isolation) and strict social-distancing and self-quarantine rules are most effective in abating the outbreak. The modeling has also produced state-specific information. For example, for New York and Michigan, isolation of persons exposed to the virus needs to be imposed within 2 days to prevent a broad outbreak, whereas for other states this period can be 3.6 days. This model could be used to determine resources needed before safely lifting state policies on social distancing. This article was included in a list of the Top 100 most highly accessed papers in Scientific Reports.

Joint work with Qin Li, Song Gao, Yuhao Kang and Xun Shi .

Manifold Learning and Nonlinear Homogenization

Published in Multiscale Modeling & Simulation, March 2022

We describe an efficient domain decomposition-based framework for nonlinear multiscale PDE problems. The framework is inspired by manifold learning techniques and exploits the tangent spaces spanned by the nearest neighbors to compress local solution manifolds. Our framework is applied to a semilinear elliptic equation with oscillatory media and a nonlinear radiative transfer equation; in both cases, significant improvements in efficacy are observed. This new method does not rely on detailed analytical understanding of the multiscale PDEs, such as their asymptotic limits, and thus is more versatile for general multiscale problems.

Joint work with Qin Li, Jianfeng Lu and Stephen J. Wright.

Semiclassical Limit of an Inverse Problem for the Schrödinger Equation

Published in Research in the Mathematical Sciences, June 2021

It is a classical derivation that the Wigner equation, derived from the Schrödinger equation that contains the quantum information, converges to the Liouville equation when the rescaled Planck constant $\varepsilon \to 0$. Since the latter presents the Newton’s second law, the process is typically termed the (semi-)classical limit. In this paper, we study the classical limit of an inverse problem for the Schrödinger equation. More specifically, we show that using the initial condition and final state of the Schrödinger equation to reconstruct the potential term, in the classical regime with $\varepsilon \to 0$, becomes using the initial and final state to reconstruct the potential term in the Liouville equation. This formally bridges an inverse problem in quantum mechanics with an inverse problem in classical mechanics.

Joint work with Qin Li.

A Reduced Order Schwarz Method for Nonlinear Multiscale Elliptic Equations Based on Two-Layer Neural Networks

Published in Journal of Computational Mathematics, March 2023

Neural networks are powerful tools for approximating high dimensional data that have been used in many contexts, including solution of partial differential equations (PDEs). We describe a solver for multiscale fully nonlinear elliptic equations that makes use of domain decomposition, an accelerated Schwarz framework, and two-layer neural networks to approximate the boundary-to-boundary map for the subdomains, which is the key step in the Schwarz procedure. Conventionally, the boundary-to-boundary map requires solution of boundary-value elliptic problems on each subdomain. By leveraging the compressibility of multiscale problems, our approach trains the neural network offline to serve as a surrogate for the usual implementation of the boundary-to-boundary map. Our method is applied to a multiscale semilinear elliptic equation and a multiscale p-Laplace equation. In both cases we demonstrate significant improvement in efficiency as well as good accuracy and generalization performance.

Joint work with Zhiyan Ding, Qin Li and Stephen J. Wright.

High-Frequency Limit of the Inverse Scattering Problem: Asymptotic Convergence from Inverse Helmholtz to Inverse Liouville

Published in SIAM Journal on Imaging Sciences, January 2023

We investigate the asymptotic relation between the inverse problems relying on the Helmholtz equation and the radiative transfer equation (RTE) as physical models, in the high-frequency limit. In particular, we evaluate the asymptotic convergence of the inverse scattering problem of the Helmholtz equation, to the inverse scattering problem of the Liouville equation (a simplified version of RTE). The two inverse problems are connected through the Wigner transform that translates the wave-type description on the physical space to the phase space, and the Husimi transform that models data localized both in location and direction. The finding suggests that impinging tightly concentrated monochromatic beams can provide stable reconstruction of the medium, asymptotically in the high-frequency regime. This fact stands in contrast with the unstable reconstruction for the inverse scattering problem when the probing signals are plane-waves.

Joint work with Zhiyan Ding, Qin Li and Leonardo Zepeda-Núñez.

Accelerating Optimization over the Space of Probability Measures

Submitted to Journal of Machine Learning Research, October 2023

Acceleration of gradient-based optimization methods is an issue of significant practical and theoretical interest, particularly in machine learning applications. Most research has focused on optimization over Euclidean spaces, but given the need to optimize over spaces of probability measures in many machine learning problems, it is of interest to investigate accelerated gradient methods in this context too. To this end, we introduce a Hamiltonian-flow approach that is analogous to moment-based approaches in Euclidean space. We demonstrate that algorithms based on this approach can achieve convergence rates of arbitrarily high order.

Joint work with Qin Li, Oliver Tse and Stephen J. Wright.

Teaching experience 1

Undergraduate course, University 1, Department, 2014

This is a description of a teaching experience. You can use markdown like any other post.

Teaching experience 2

Workshop, University 1, Department, 2015

This is a description of a teaching experience. You can use markdown like any other post.